Blad, steen, schaar met velen

Binnenkort is het startdag van de chiro en ik gok dat dan het aantal spelletjes Blad, Steen, Schaar (nee het spel heet niet anders… ) aanzienlijk stijgt in ons Belgenlandje. Je kan Blad, Steen, Schaar of RPS (Rock, Paper, Scissors) met twee spelen of in grotere groepen. Als je in groepen speelt van toenemende grote wordt de kans om nog winnaar(s) aan te duiden steeds kleiner. Maar hoe klein juist?

Deze blogpost onstond, zoals veel mooie dingen, op chirokamp met Chiro Spirit Heverlee. Daar werd ik door mede-koki Luke ge-nerd-sniped. In dat gesprek met Luke kwam de uitdaging bovendrijven om te berekenen hoe klein de kans is om een winnaar aan te duiden als we met heel ons chirootje (ongeveer 60 m/v/x sterk) speelden. Dat wou ik dus wel eens uitdokteren.

Op kamp probeerde ik met wat hoofdrekenen (niet mijn sterkste kant) en kwam ik er echt niet uit. Zo leerde ik weer dat het probleem op papier zetten helpt. Wat ik verder nodig had om dit telprobleem op te lossen was echte wiskunde: probleemoplossend redeneren met een vleugje speltheorie en kansrekenen.

Probleemstelling

Voor we formules boven halen en beginnen te rekenen, moeten we eerst ons probleem goed uitschrijven. Ik stel dit voor als probleemstelling:

Wat is de kans om in een enkelvoudig spelletje Blad (P), Steen (R), Schaar (S) met een groep van g spelers winnaar(s) aan te kunnen duiden?

We spelen dus niet tot er maar 1 winnaar overblijft, een groep winnaars is goed genoeg. (Deden we dat wel dan wordt het complexer, misschien iets voor een volgende blogpost?) Laten we dus, om eenvoudig te beginnen, eerst kijken naar RPS met $g=2$ spelers en tellen hoeveel mogelijkheden er zijn om te winnen. Als we dat delen door het totaal aantal mogelijkheden dan kennen we de kans om te winnen.

Als dat gelukt is gaan we hetzelfde doen voor 3 spelers en proberen we een formule te vinden om de kans te berekenen voor eender welk aantal spelers. Met die formule kunnen we dan de kans berekenen voor $g=60$.

RPS met 2 spelers

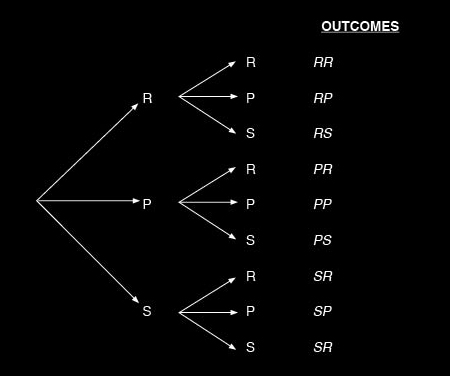
We kunnen het spel visueel voorstellen door elke speler een letter R, P of S te laten kiezen. In de illustratie hieronder (een spel-boom) heeft elke speler een niveau met daarin zijn keuzes opgelijst. Aan de hand daarvan kunnen we makkelijk de mogelijkheden tellen voor dit geval.

(De afbeelding heb ik hier gevonden en zo geinverteerd.)

Voor het spel met $g=2$ waarbij elke speler (P1 en P2) drie opties heeft zijn er in totaal $T(2) = 3 \cdot 3 = 3^2 = 9$ opties. Dat kan je makkelijk zien in de bovenstaande afbeelding en die telling geldt logischerwijs (inductief te bewijzen) ook voor grotere g. Dat geeft ons als formule voor het totaal aantal opties:

++T(g) = 3^g++

Bij RPS met $g=2$ is er slechts 1 manier om gelijk te spelen nl. beide dezelfde keuze maken (RR, PP, of SS). Dat zijn dus Daarvan 3 opties die tot een gelijk spel leiden en dus 6 die een winnaar aanduiden. Die 6 ($= 3 \cdot 2$) opties kan je ook als volgt bekijken: voor een winnend spel heeft P1 3 opties en heeft P2 daarna nog maar 2 opties (want hetzelfde als P1 kiezen leid niet tot een winnend spel). Dat in de realiteit die keuze tegelijkertijd wordt gemaakt maakt voor het tellen van de opties niet uit. Of nog anders bekeken: tel de winnende opties in 1 tak van de boom en vermenigvuldig met 3 omdat er 3 gelijkaardige takken zijn.

Dat betekent dat er voor $g=2$ een kans is van $\frac{W}{T} = \frac{6}{9} = 66\%$ om een winnaar te kunnen aanduiden. Dit kan je zelf makkelijk experimenteel testen door met twee veel spelletjes RPS te spelen en te tellen hoeveel er worden gewonnen en dat delen door het totaal spelletjes. Als je genoeg spelletjes speelt kom je heel dicht in de buurt bij 66% winnende spelletjes.

RPS met 3 spelers

Voor $g=2$ was het tellen makkelijk: binnen enkele minuten heb je alle opties opgeschreven en geteld. Dat wordt al iets moeilijker voor $g=3$ het zijn er immers $T(3) = 3^3 = 27$. Voor nog grotere g is dat al helemaal lastig. (De g staat namelijk in de exponent van de 3, en zo’n functie 3^g stijgt zoals je mogelijk weet razend snel.) Maar met het inzicht dat we voor $g=2$ kregen en het systeem om de keuzes met letters voor te stellen moet het tellen wel lukken.

Voor $g=3$ is er echter nog een extra manier om gelijk te spelen. Namelijk als de 3 spelers elk een verschillende keuze maken (bvb RPS of PSR). Daar moeten we in onze telling ook rekening mee houden.

Gelijkaardig als bij het spel met twee spelers kunnen we in 1 tak van de boom (bvb. R) de winnende opties tellen en die maal 3 doen (dat kan omdat elke keuze evenveel winnende keuzes heeft, het spel is symmetrisch). Nu komt het erop aan om die opties op een slimme manier te tellen zodat we dat systeem ook voor grotere g nog kunnen (als de boom tekenen helemaal onmogelijk wordt). We tellen dus enkel de winnend opties als P1 R kiest. Die zien er in onze notatie uit als R??. Op de vraagtekens kunnen dan nog R,P en S komen en de totale lengte van het ‘woord’ is 3 letters omdat het spel 3 spelers heeft.

Nu moeten we zoeken naar een structuur die je kan veralgemenen (in functie van het aantal spelers). Gelukkig moet je voor veel wiskundige problemen niet zelf van nul starten.

(Van nul starten dat kan wel leuk en interessant zijn, zo ben ik er alleszins ook aan begonnen. M’n initiële formule had ik zelf proberen af te leiden zonder een formularium te gaan raadplegen. Tevergeefs: m’n formule gaf voor $g=70$ nog steeds een kans van 50 procent. Als je zelf in grotere groepen al eens RPS gespeeld hebt dan weet je dat dat niet kan kloppen. Dan maar de oplossing zoeken met een formularium.)

Met een zetje in de goede richting met behulp van dit telproblemenformularium friste ik m’n kennis wat op om de opties slim te tellen. Als P1 R kiest zijn de volgende opties nog goede opties die we in twee gevallen Ra) en Rb) onderscheiden:

Ra)

• RR 0 keer een P kiezen NIEMAND WINT -> niet tellen
• RP 1 keer een P kiezen
• PR 1 keer een P kiezen
• PP 2 keer een P kiezen

Rb)

• RR 0 keer een S kiezen NIEMAND WINT -> niet tellen
• RS 1 keer een S kiezen
• SR 1 keer een S kiezen
• SS 2 keer een S kiezen

Als we naar geval Ra) kijken en dat naast het formularium houden dan kunnen we daarin een herhalings-variatie (‘Variation with repetition’, n-tuple) herkennen. We willen namelijk het aantal woorden tellen van 2 letters ($= g-1$, want P1 koos R) gekozen uit ${R,P}$. Dat zijn RR RP PR en PP. Er is echter 1 probleem: de optie RR die geldig is als herhalingsvariatie is geen optie die we willen meetellen omdat niemand het spel RRR wint. Daarom zijn het aantal opties voor Ra)$ = V^2_{g-1} -1 = 2^2 - 1 = 3$

Nu we een formule voor Ra) hebben zijn we klaar voor $g=3$. Want door het opsplitsen in gevallen en de symmetrie in het spel hoeven we de andere opties Rb) of ook Pa) en Pb) niet apart te tellen. Er zijn evenveel opties in a) als in b) en in elk van de 3 takken voor speler 1 ook. Dat geeft ons de onderstaande formule:

++W(g) = 3 \cdot 2 ( 2^{g-1} - 1)++

Voor g > 3 komen er geen nieuwe manieren bij om gelijk te spelen. Dat betekent dat onze telling ook geldt voor grotere g. Je kan het probleem immers systematisch herleiden tot de bovenstaande formule wat neerkomt op

1. Splits op in drie gevallen voor speler 1 (tel 3 keer stap 2))
2. Splits elk geval op in twee opties een a en b afhankelijk van de verdere keuze van een S of P. (tel 2 keer stap 3)
3. Tel het aantal herhalingsvariaties in Ra) minus het geval altijd hetzelfde te kiezen.

Conclusie

Om nu de kans te weten dat je met een groep van 60 nog een winnaar kan aanduiden in het RPS spel, vullen we de formule in ($W(60)$) en delen we door het totaal aantal opties $T(60)$. Dat geeft dan:

++\frac{W(g)}{T(g)} = \frac{3 \cdot 2 ( 2^{g-1} - 1)}{3^g}++

++\frac{W(60)}{T(60)} = \frac{3 \cdot 2 ( 2^{60-1} - 1)}{3^{60}} = 8.1591649 \cdot 10^{-11}++

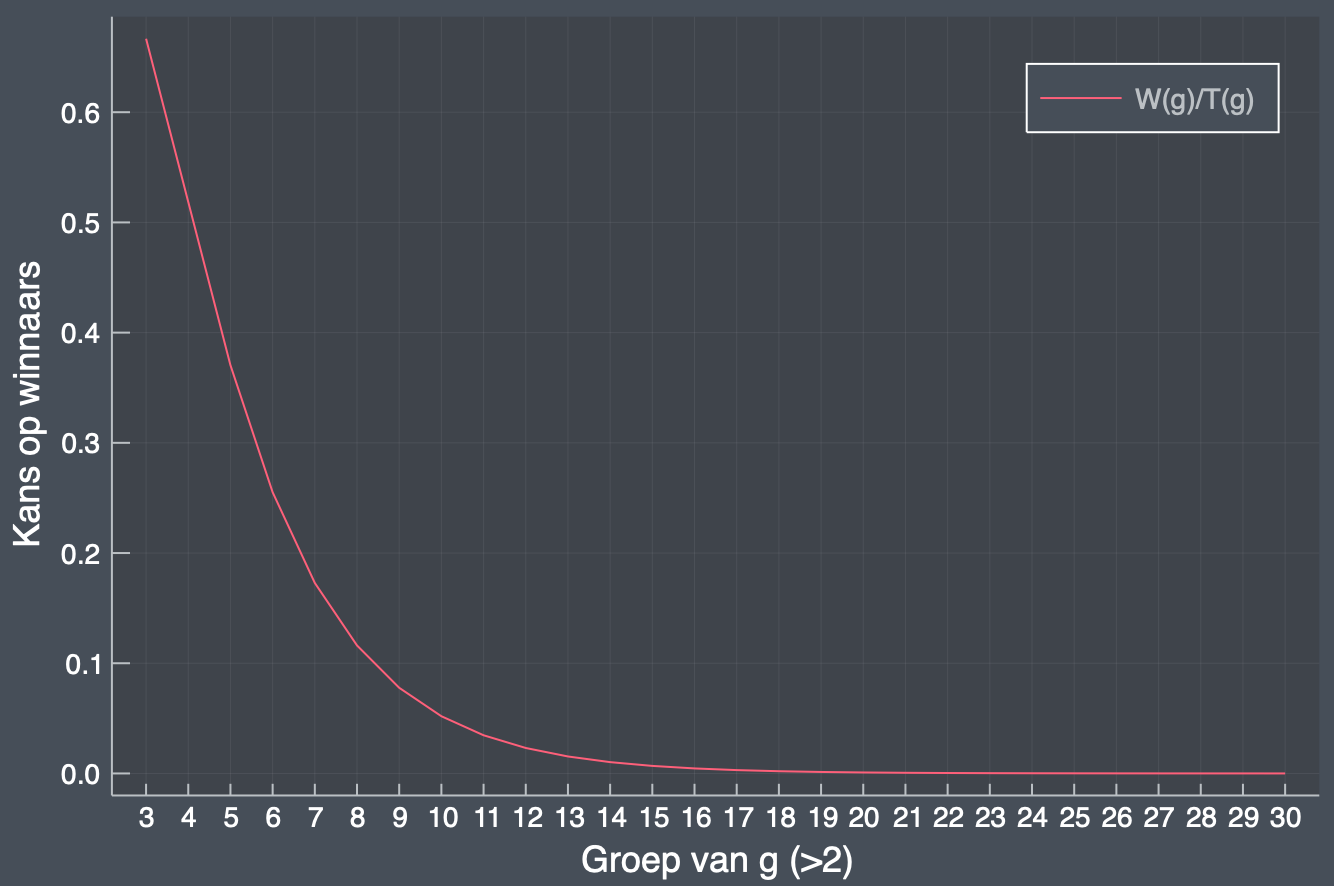
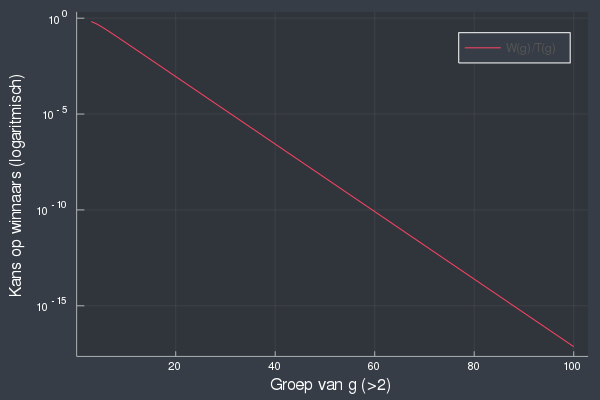
Dat is dus een astronomisch kleine kans. Onbevattelijk klein. Zelfs 1 op 1 miljard kans, $10^{-9}$, is nog 100 keer waarschijnlijker dan dit. Hieronder kan je tot slot twee grafieken van de functie zien. Die kan je nu gebruiken om in te schatten met welke grootte van chirogroep je blad, steen, schaar nog redelijkerwijs kan spelen.